A probability question: Fast Duelers

• Duels in the town of Discretion are rarely fatal
• There, each contestant comes at a random moment between 5am and 6am  on the appointed day, and leaves exactly 5 minutes later, honor served,  unless his opponent arrives within the time interval and then they fight
• What fraction of duels lead to violence?

Solution:

We divide solution space into mutually exclusive 3 cases. Let's call duelers John, Mike.  The first case  is when John comes between  5:05-5:55; the second case is when John comes between 5:00-5:05 and the final case is when John comes between 5:55-6.00.

Case 1:

So John arrives somewhere between 5:05-5:55

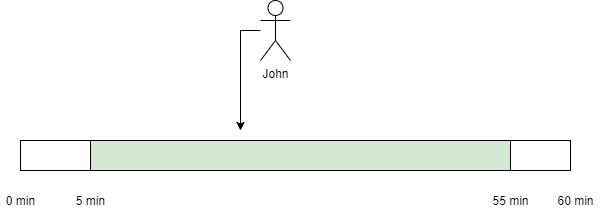
Now Mike has only a small 10 mins window where he can come across with John. This is 5 mins before John till 5 mins after.

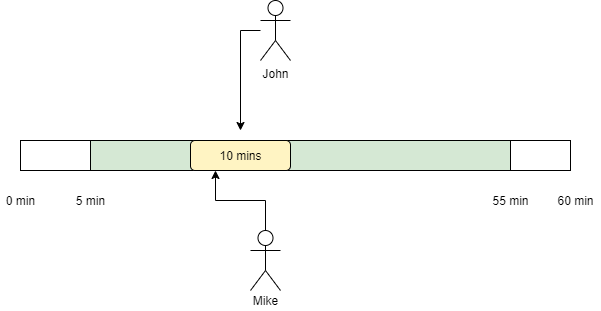
So the probability of this happening is :

$ P(case1) = P(Yellow) \times P(Green) = \frac{50}{60} \times \frac{10}{60}  =\frac{5}{36}  $

Case 2:

Case 2 is when John arrives the first 5 mins. In this case if Mike arrives between 5:00 till after 5 mins when John arrives there will be a collision.

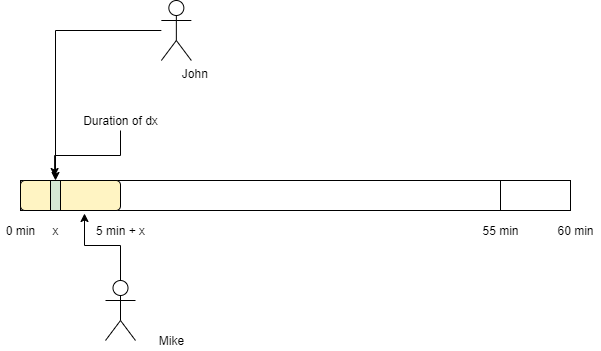
We need integrals to calculate this.

$P(case2) = P(Yellow) \times P(Green) = \int_{0}^{5} \frac{x+5}{60} \times \frac{dx}{60} = \frac{3}{288}$

Case 3:

Actually case 2 and case 3 are just symmetric. But let's not be too lazy and find this part as well.

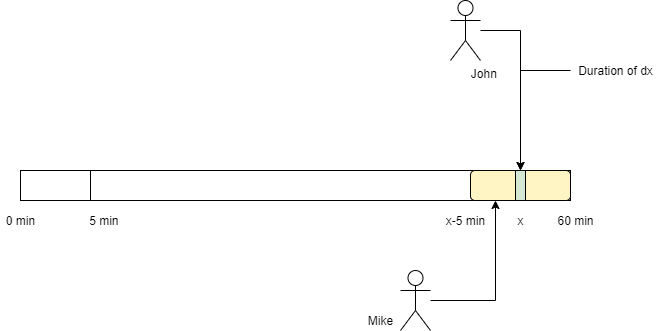
$P(case3) = P(Yellow) \times P(Green) = \int_{55}^{60} \frac{60 - (x-5)}{60} \times \frac{dx}{60}=\frac{3}{288}$

Finally

$P(conflict) = P(case1) + P(case2) + P(case3) = \frac{23}{144}$

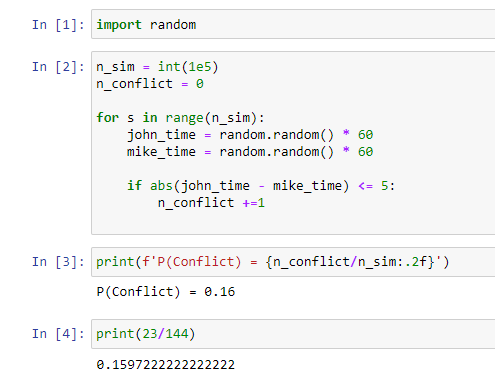
Let's code this: