An interesting probability question: Box collection

Recently I read about a nice probability question and was thrilled about it. It is not that the question is hard but it is because the question really teach about a fundamental issue in probability. So I wanted to both solve the problem and do a Monte Carlo simulation to verify.
Problem:
- There are cereal boxes numbered 1 to 5 only possible to see after opening the box. A set of one of each number is required to win a price. Knowing that each number is equally likely, how many boxes on average are required to make a complete set?

Solution:
The trick in this question is to define the problem in a nice way using a mathematical description.
Let's say $T_{1}$ is the number of boxes it takes to get first distinct number and $T_{2}$ is the number of boxes it takes to get the second distinct number after getting the first one. Thus if $T_{win}$ is the number of boxes to get the prize,
$ E(T_{win}) = E(T_1 + T_2 +T_3 + T_4 +T_5)$
Here it is important to see that $T_1, T_2, T_3, T_4, T_5$ are independent. Thus
$ E(T_{win}) = E(T_1) + E(T_2) + E(T_3) + E(T_4) +E(T_5)$
Also note that each of this random variables are coming from a geometrical distribution. I.e
$P(T_k = n) = p \times (1-p)^{(n-1)}$
where p = 4/5 for k=2, p=3/5 for k=3, p=2/5 for k=4 and p=1/5 for k=5.
Since expected value of a geometric random variable is 1/p,
$E(T_1) = 1$, $E(T_2)= 5/4$, $E(T_3)=5/3$, $E(T_4)=5/2$, $E(T_5) =5$
Thus,
$E(T_{win}) = 1 + 5/4 + 5/3 + 5/2 + 5 = 137/12$
Simulation:
Let's code this up!
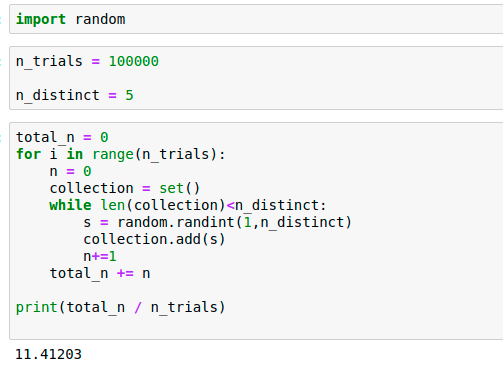
See also:
