Machine Learning in Production Series 2 - Deployment & Monitoring

In my journey to learn more about ML on production, I am taking Machine Learning Engineering for Production (MLOps) Specialization from Deeplearning.ai . In this blog post series, I will try to summarize my learnings as a way to review myself. Almost all of the visualizations I will use in this post are sourced by the presentations in the specialization.
In this second post of the series, I will be focusing on modeling and deployment step of the ML production life cycle. If you haven't read the first writing describing the first 2 steps, I suggest you to read it.
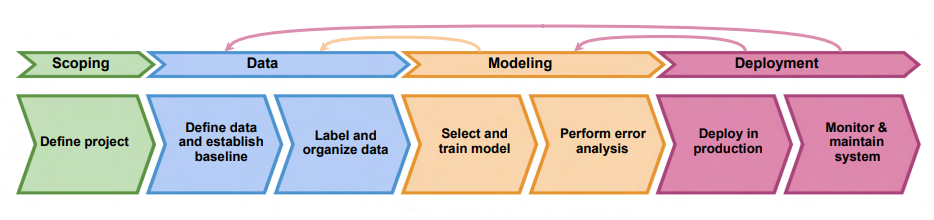
Modeling
Modeling is the part where we build ML code. Here we need to decide on the type of the model which would fit the best to the problem at hand. However one should be aware of the fact that this step is not only about optimizing accuracy or minimizing error but it is crucial to make sure model is performing well on different critical scenarios. Also we need to make sure that the model is not discriminating ethnicity, gender, language or etc. For a nice reading about ethical AI checkout one of my earlier posts.
In his lectures, Andrew Ng suggests to be fast on finding a model. He recommends to start with , if possible, an already known open-source model. This is because this model can help as a baseline and could guide through both on data and possible direction on other models.
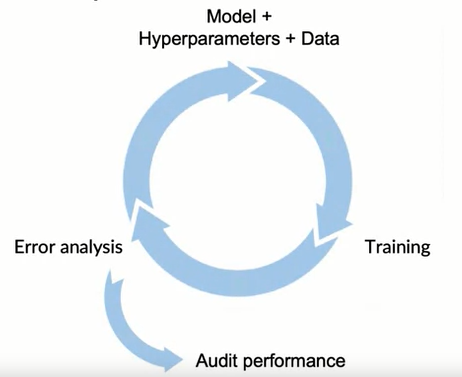
Error Analysis
Error analysis is the step where we try to understand the model and how it fails. There is no clear way of doing this and it might require domain expertise. However, the point here is to find the scenarios where our model is failing significantly and try to fix it for example by adding more labeled data for the scenario.
Error analysis could be done using a simple spread sheet. An error analysis of a speech recognition system could look like below.

Deployment
There are many decisions/challenges when it comes to deploying. Some of the challenges are as follows:
- Is the model going to work real time or batch style
- Is the model will be served on cloud or browser
- What are the compute resources (CPU / GPU / memory) ?
- What is the target latency?
- How we will deal with the logging?
- How we will deal with the security issues?
- How do we monitor production performance for taking action against possible concept drift and data drift?
Deployment Patterns
There are different deployment patterns depending on the maturity / risk - criticality of the model. Some of the patterns are as below:
Shadow Mode Deployment
This is when we run the model in parallel to human judgement. Here the model basically shadows the actual work. This is done to be able to compare model performance without making any critical error.
Canary Deployment
At this type of deployment, a small fraction of the trafffic (say 5%) goes through the newly built model while main fraction still uses already existing solution. After the new model proves to be robust traffic is ramped up gradually. The name "Canary" comes from English phrase canary in coal mine which was a way of spotting if there was a gas leak in coal mine.
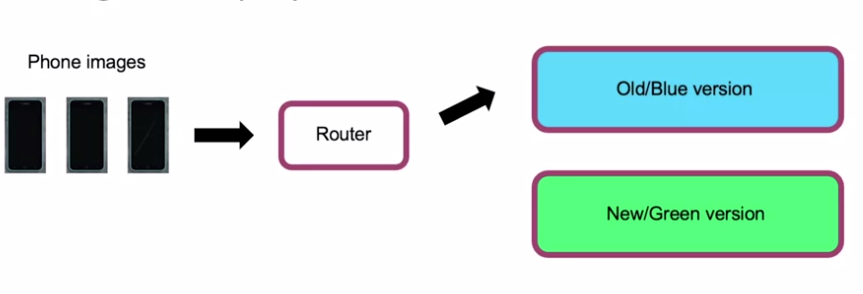
Blue Green Deployment
This is a very intuitive deployment pattern where the traffic is controlled by a router. The old and the new models is expected to have exactly the same inputs and outputs. This way, router can switch the traffic to the new model. Moreover if anything goes wrong it is possible to roll back to old version easily.
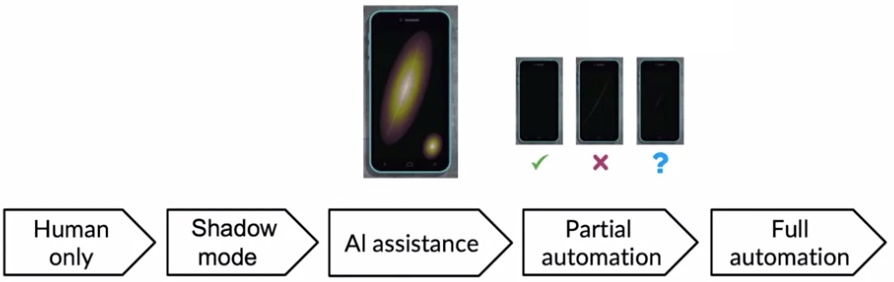
Degrees of automation
Automation could be done in different degrees depending on the nature of the task. In some application full automation where AI is responsible of the whole process is the way to go. In some other applications, AI might be more suitable to assist a human. For example for a task of detecting phone screen defects different version, full automation classifies defects without any intervention while AI assistance helps human labor by highlighting possible defects for easier human procession. Another type of automation is partial automation where AI handles easier cases where confidence is high but consults to human judgement for harder low confidence cases.
Monitoring
After successfully deploying the model, we need to constantly monitor it to make sure of continuous quality. Some of the metrics to monitor could be as below.
- Software metrics
- Memory, latency, server load
- Input metrics
- Average input features
- Missing values
- Output metrics
- Usage metrics
- Average output
This concludes the review of the first course "Introduction to Machine Learning in Production". This course was generally high level talking about the principles instead of being practical. I will be following rest of the courses in the specialization and will be writing about new learning in the following posts of this series.
