An interesting probability question: "Flat Tires"

The other day we were having lunch with one of my very smart colleagues. He had a very interesting problem. So he was travelling with his car when his car alarmed that one of the tires is flat. He went out and checked 3 tires but all of them are just fine. So what is the probability that the last tire is actually flat? Should he be worried about? 100% right? Well no. Because the system has a certain false positive rate. So we should take that into account.

Well let's take this to the extreme cases. If false positive rate is fp and if  there is only 1 tire then the probability that the last tire is flat is basically fp.  On the other hand if there are, let's say 10 thousand tires and you checked all of them but the last one then well probably this was a false positive case.

In reality it is rarely possible to know false positive rate beforehand. Actually an even more interesting question is to estimate fp by checking the tires where the system alarmed. However let's leave that challenge for another day and assume we know fp and we want to know probability of false positive given that the system alarmed and we checked all but the last tire.

Problem:

With a car which have an alarm system of false positive rate of "fp" and  n tire, what is the probability that the last tire is flat given that the system gives an alarm and you checked all but the last tires and they are fine?

Solution:

Let's first start with some definitions

fn:  nth tire is flat

ownf : The system alarmed we checked n-1 tire and they are alright

$P(fp)$ : The probability that the system gives false positive (false positive rate)
-----------------------------------------------------------------------------------------------------

The question :

$P(fn | ownf)$

By Bayes rule ->

$P(fn | ownf) = \frac{P(ownf | fn) \times P(fn)}{P(ownf)}$

Last get each element one by one

1)

Since we assume system will surely catch true positive:

$P(ownf | fn) = 1$

2)

$P(ownf) = P(ownf | fp) \times P(fp) + P(ownf|\sim fp) \times P(\sim fp)$

Since when the case is false positive, we always need to check first n-1 wheels, thus:

$P(ownf | fp) = 1$

When we know the case is not a false positive, the probability that we check all 3 wheels and they are alright, can only happen if the flat tire is the last thus:

$P(ownf|\sim fp) = P(fn|\sim fp)  = 1/n$

$ P(fn|\sim fp) =  (1-P(fp))$

$P(ownf) = 1 \times P(fp) + 1/n \times (1-P(fp))$

3)

$P(fn) = P(fn | fp)\times P(fp) + P(fn | \sim fp) \times P(\sim fp)$

Since given that the case is  false positive, there is no probability that last wheel is flat. So:

$P(fn | fp)= 0 $

$P(fn) =  P(fn | \sim fp) \times P(\sim fp)$

From 2)

$P(fn) = 1/n \times (1-P(fp))$

Now we have all, so the result is:

$P(fn | ownf) = \frac{1/n \times (1-P(fp))}{P(fp) + 1/n \times (1-P(fp))}$

This result is actually quite intuitive. This is because you only check all the $n-1$ first tires if either the alarm is a false positive or if the alarm is true positive and the last tire is flat.

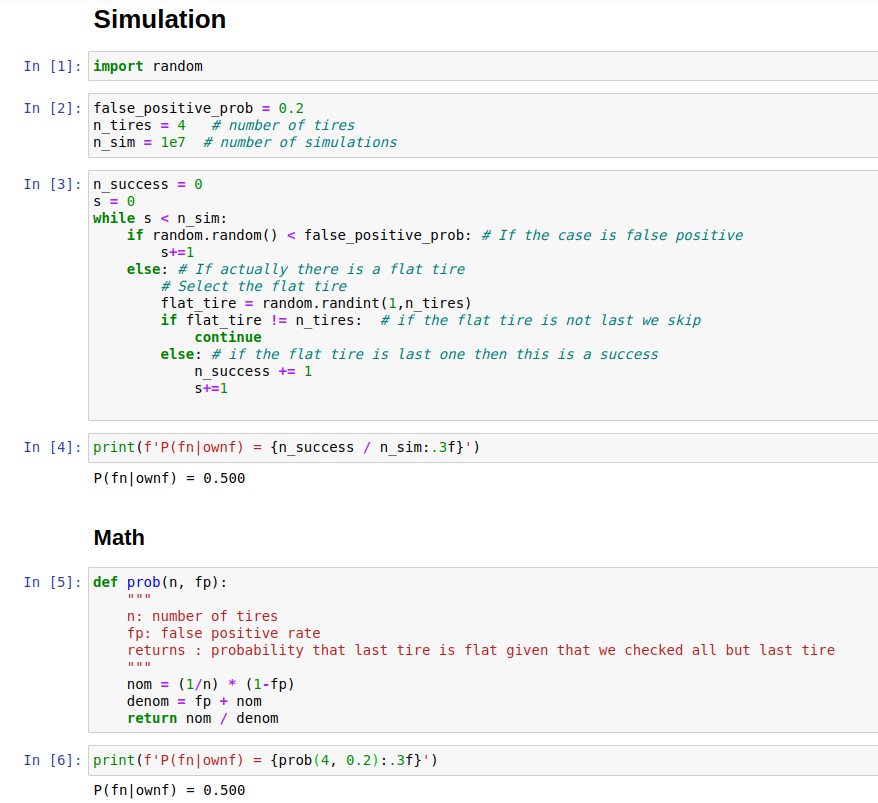
So if P(fp) = 0.2 and your car has 4 tires:

$P(fn|ownf) = \frac{1/4 \times (1-0.2)}{0.2 + 1/4 \times (1-0.2)} = 0.5$

But if it had 100 tires:

$P(fn|ownf) = \frac{1/100 \times (1-0.2)}{0.2 + 1/100 \times (1-0.2)} = 0.038$

Let's code :