An interesting probability question: Gambler's Ruin

Okay here comes a nice question on probability. (Please mind your random steps =))
Problem:
There are 2 gamblers. Joe has 10 dollars in his pocket and Peter has 2 dollars. They always play with 1$ each game. We know that Peter is better than Joe when it comes to dices he has a probability of winning 2/3. If they play till one of them goes bankrupt what is the chance that Joe will win?
Solution:
From Peter's point of view this problem is a random walk. We step +1 with a probability of 2/3 and -1 with 1/3 probability. Random walk starts from 2 and will end either at 0 or 12. For a more general solution let's assign winning probability to $p = 2/3$ (Peter wins) and $j=1/3$, $M=2$ and $N=10$.
Now let's say that Peter's probability of stepping back is $P_{X}$ when his money equals X including all paths(i.e 1 forward 2 backward). For a moment let's say Joe has infinite money. Assuming M→∞ having a step back does not depend on the location X. Thus
$ P_{X} = P_{X-1} = P$
Now let's find P. The probability of ever stepping back is either step back directly or step forward once and step back twice. So
$ P = (1-p) + p \times P ^ 2 $
The solution of this equation forms the following graph.
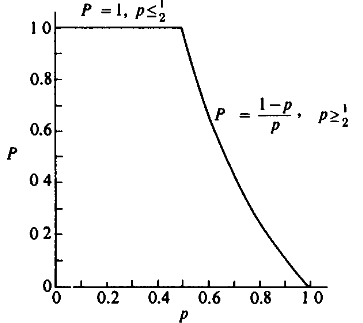
This is actually very interesting. In this conditions, for Peter to lose, he needs to step back N times which is of probability $(\frac{1-p}{p})^ N)$ otherwise games just never ends.
So Peter loses with probability $(\frac{1-p}{p})^N) $. Of all his losts there are 2 possibilities. Either he reaches M+N and loses or never reach there. If the probability of never reaching there (Joe winning) is $Q$, then.
$(\frac{1-p}{p})^N = Q + (1-Q) \times (\frac{1-p}{p})^{M+N}$
Now we got everything.
$P_{Joe} =1 - \frac{1 - (j/p)^N}{1 -(j/p)^{M+N}}$
Fantastic, now plug in the numbers.
$P_{Joe} = 1- \frac{1- 0.5^2}{1 - 0.5^12}$
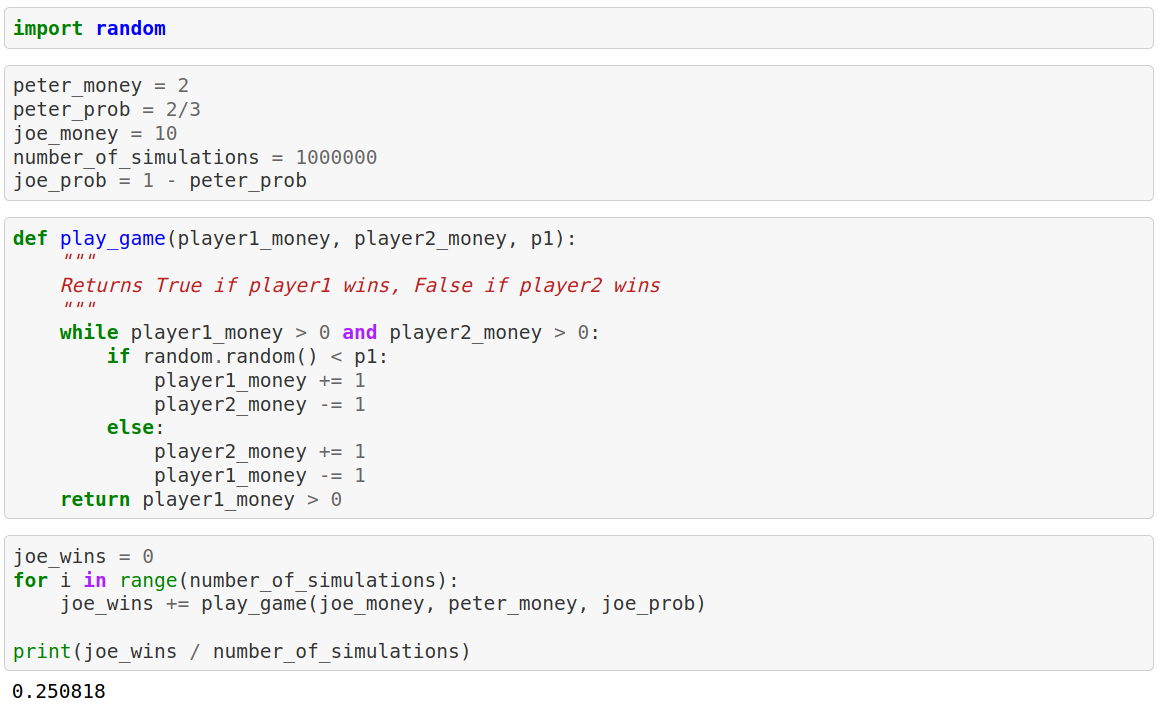
$ P_{Joe} = 0.25
More than you would expect right? Okay now let's make a Monte Carlo simulation to confirm this result.
See also:
https://en.wikipedia.org/wiki/Gambler%27s_ruin
http://www.columbia.edu/~ks20/FE-Notes/4700-07-Notes-GR.pdf
